| RESOURCE MATERIAL for the EINSTEIN CENTENARY (2015) |  |
|
PITP/ST-JOHNS PUBLIC LECTURES, 2014 -2015 |
|
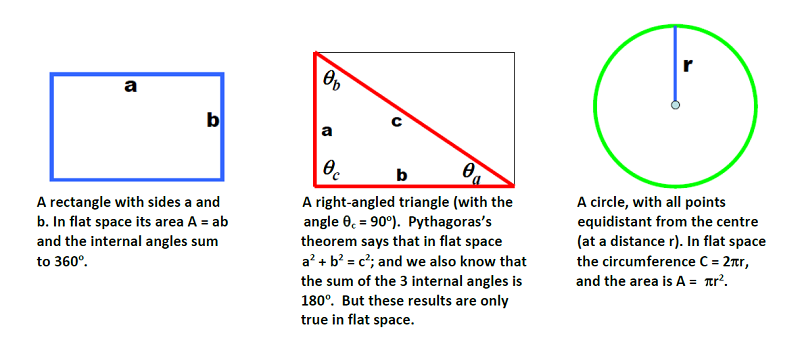
Curved Spacetime One of the things that leaps to mind when Einstein is mentioned is the idea of 'curved space', and its association with gravity. Let's see if we can understand this in a simple way. Suppose we look first at some curved balloon surface - this is a 2-dimensional surface which we see in our own 3-dimensional space. Now when a mathematician or physicist talks about "curvature" for some surface, what they really mean is stretching or twisting in a way which changes angles and distances between points in the surface. If we look at the surface from outside (ie., from the vantage of our own 3-d space) it is easy to see if this is happening - we could, eg., paint some object on the surface, and see if its shape distorts. Suppose, however, that we do not live in 3-d space, and that our entire experience is confined to the 2 dimensions of the surface - we don't even know that there exists a world outside the surface, and have no means of doing so. How can we tell, from inside, whether our space is "curved" or not? In fact there is only one way: we have to make measurements - of lengths, angles, and so on - and see whether the results agree with what we would get if the space was "flat". Now objects in a flat space obey things we all take for granted - like, eg., Pythagoras's theorem, or the idea that 2 parallel lines never meet, always staying the same distance apart; or that the area of a square of side L is equal to L2. And certainly we expect that the sum of the internal angles of a triangle is 180 degrees. But if we are 'stuck' inside the surface, how can we check these? It is not as if we can "look down on the triangle from outside"; because for us there is no outside. |
|
|
The answer is that the only way to do this is to make measurements of geometric objects like those shown above. To see what will happen if the surface is NOT flat, let's look at what we would get if now tried to make such measurements on a "curved" surface. This is easy - we can look at a spherical surface. |
||
|
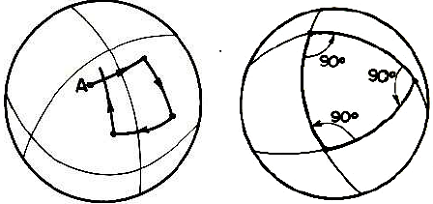 ABOVE LEFT: What happens if we try to make a square on a sphere, with 4 right angles & equal sides. ABOVE RIGHT: A triangle in a spherical surface - the angles do not add up to 180 degrees. |
|
Again, you must resist the temptation of thinking in 3d here - imagine that our being cannot sense anything outside the 2d surface. From the pictures above, we see that by doing simple measurements a 2-dimensional being can figure out if it is living in a curved or a flat geometry. But it is not allowed to "look at" these figures from "outside". What now of us? We of course do not live in 2 dimensions - indeed, as understood by Einstein and Minkowski, our world is the 4-dimensional one of spacetime. Now again, it is crucial that we cannot tell "just by looking" to see if our spacetime geometry is flat (to do this, we would have to live in 5 dimensions or higher). All we can do is make measurements to see if the spacetime we live in is flat or not. So, what do we find? One of the key insights in Einstein's extraordinary General Theory of Relativity is that spacetime is indeed curved, and that this curvature has to do with gravity - in fact, in a certain sense, gravity IS spacetime curvature. What is more, the cause of the curvature turns out to be energy (more precisely, what physicists call 'stress-energy'). It is for this reason that we see gravitational fields around matter - matter itself contains energy, according to the famous relationship E = mc2. But when we look for spacetime curvature, it is very hard to find - it was only after Einstein's theory that it was realized that even very small curvatures are equivalent to enormously strong gravitational fields. Finally, in 1919 the famous solar eclipse expedition led by Eddington and Crommelin succeeded in seeing the tiny deflection of starlight beams caused by the sun. This was not actually the first piece of evidence for Einstein's theory - this came when Einstein himself, in 1915, calculated the very small 'perihelion precession' of Mercury's orbit around the sun (shown in the Figure below) that came from spacetime curvature caused by the mass/energy of the sun. He found his calculated result to agree beautifully with the result that had been already measured (and for which there was no good explanation until that time). But even the enormous mass of the sun leads to miniscule effects. |
||
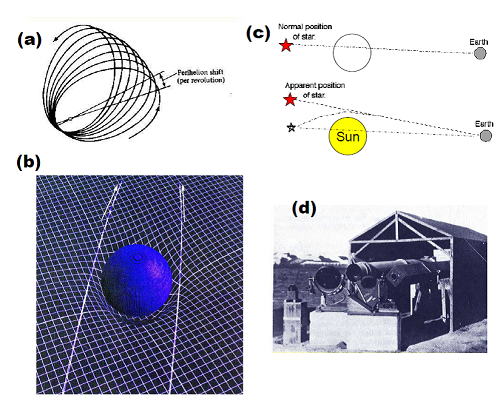 Early tests of the General Theory of Relativity. In (a) we show schematically the precession of the orbit of Mercury (greatly exaggerated). In (b) the bending of two light beams around the sun is shown (again exaggerated); and in (c) we show how this leads to a shift in the apparent position of a star behind the sun. In (d) one of the telescopes used in the 1919 solar eclipse expedition is shown. |
||
It took a long time before it was realized by astronomers that very strong gravitational fields, capable of causing huge distortions of spacetime, were out there waiting to be found in the universe. In this respect our own solar neighbourhood is a very quiet backwater. The story of how all this was discovered, and what kind of phenomena can now be observed, is one of the most fascinating and spectacular in all of science - see here. If you want to read more on curved spacetime, go to GR-Spacetime, and/or to articles on Wikipedia.
|
||
|
||