| RESOURCE MATERIAL for the EINSTEIN CENTENARY (2015) |  |
|
PITP/ST-JOHNS PUBLIC LECTURES, 2014 -2015 |
|
Black Holes Black Holes are perhaps the strangest objects to have ever been predicted by physics. For many decades they were the 'bad actors' of Einstein's theory of Gravity, the "General Theory of Relativity". It was realized as early as 1932 by Chandrasekhar and by Landau that if a star exceeded a certain mass, then once it had run out of fuel it would have to collapse, and that in principal, IF one believed Einstein's theory, it would collapse into a point singularity, at which the gravitational field became infinite. Further investigation of this was done by Oppenheimer, Snyder, and Volkoff in 1938, but the general opinion of most physicists and astronomers (including Einstein himself) was that one should NOT believe the theory - the predictions were just too far out to be believable. Thus it was that in the period between 1938-1963, only a very few theoretical physicists (principally Lifshitz, Khalatnikov, and Landau in Moscow) were prepared to seriously investigate such singularities. The assumption of most (but not all) other physicists was that something (rotation of the systems, or matter, or whatever) would prevent the singularity from existing - it was too much of an abomination. And besides, Einstein had rejected them - this was enough for most scientists. A radical shift occurred within a few years, between 1964-70, for 2 reasons:
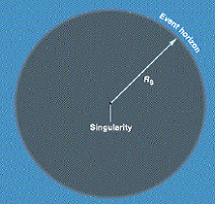
So what is a black hole? In curved spacetime we see that energy causes spacetime to curve. But energy does not just come in the form of matter - indeed, spacetime curvature itself has energy (rather like the energy in a coiled spring), even if there is no matter around. Now since this curvature can attract more energy (it exerts a gravitational force on any other matter or energy nearby), we can get a runaway process occurring in which the energy density in some part of spacetime, and hence the curvature, increase without limit. The result is a 'spacetime singularity' where the 'stretching/twisting' of spacetime becomes infinitely large. For this to happen we need to start off with a very large initial concentration of mass/energy - as we will see below, the most common way to initiate this is to start with a supergiant star, which then collapses once it has exhausted its fuel. Since, as we saw in curved spacetime, we cannot 'stand outside' 4-dimensional spacetime, we cannot easily visualize what is happening to spacetime around a black hole. But we can draw schematic pictures. Let's first look at what is called a "Schwarzchild black hole"; this is one which is not rotating. It has a central singularity, where the 'stretching' of spacetime becomes infinite. This singularity is enclosed by a spherical region from which nothing can escape, even light. The radius of the sphere, called the Schwarzchild radius, is proportional to the mass of the object - a non-rotating black hole with the mass of the sun would have a Schwarzchild radius of about 3 km. Note there is nothing physically there at this spherical surface, which is called the 'event horizon' - it simply marks the boundary between the inner region, from which nothing can escape, and the rest of the universe. Anything approaching the event horizon will be very strongly attracted to the black hole, but if it is moving fast enough, it can still avoid falling below the event horizon - we see this with the light rays shown below. Light passing far from the black hole has its path bent only weakly by the curvature of the spacetime, but if it goes through the event horizon, it falls inexorably to the singularity (meanwhile being stretched along with the spacetime). Anything else going in is also stretched - typically to destruction, with the liberation of lots of energy as it goes in. |
|
|
 Paths of light rays moving past a Schwarzchild black hole. The hatched circle marks the event horizon; nothing passing inside this can escape. |
|
|
Now any real black hole is rotating, and indeed most of them are rotating extremely fast. The structure of a rotating black hole, the "Kerr" black hole, is much more complex. Now spacetime is stressed in a more complicated way - it is not only stretched but 'twisted' around the axis of rotation. A light ray passing near to such a black hole can follow a very tortuous path indeed (see Figure below). It turns out that there are 2 important surfaces or event horizons for a Kerr black hole, and one is only completely trapped below the lowest spherical one. There is actually a ring-shaped singularity inside this, and the spacetime structure has a peculiar hourglass or 'throat' structure, illustrated schematically in green below. |
||
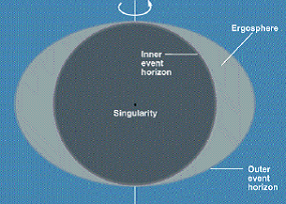
The event horizon structure of a Kerr black hole. Between the inner and outer event horizons is the 'ergosphere'. |
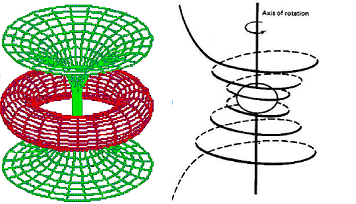 ABOVE LEFT: In red, the ring singularity inside the event horizon of a Kerr black hole; in green, the spacetime structure. ABOVE RIGHT: path of a light ray passing near to a Kerr black hole. |
|
Remarkably, the Kerr solution describes real black holes very well - it has now become the basis of much science fiction speculation about travelling through wormholes, etc. But, science fiction aside - why should we care about all of this? In fact, we now know that it is quite impossible to understand the really key features of the universe, as it exists today, without appealing to black holes. At the centre of all major galaxies lies a "supermassive black hole", with masses ranging from a few million solar masses up the largest so far found, with a mass of 30 billion suns (and there will be certainly be larger ones found in the future). Even the small ones have a major effect on the evolution of their host galaxy (the mass of our own Milky Way black hole is a puny 4.3 million suns); the big ones have a really drastic effect. As an example, consider the monster galaxy M87, the largest galaxy in the "Virgo supercluster" of galaxies, around which our own local group of galaxies moves. This colossal galaxy has a mass of some 3 trillion suns (ie., nearly 40 times greater than the Milky Way mass - and the Milky Way is itself a giant galaxy!), with a supermassive black hole at its centre, of mass estimated to be 6.7 billion suns. The huge high-energy jet emerging from the central black hole, along with shock waves emanating from its vicinity, have heated the gas throughout the galaxy to 2 million degrees - effectively the central black hole has sterilized the whole galaxy, and it doubtful that any planets exist there. We should be thankful that the Milky Way black hole is so small! |
||
 ABOVE LEFT: The monster galaxy M87, at a distance of 55 million light yrs from us, with many smaller satellite galaxies around it. ABOVE RIGHT: The ultra-relativistic jet emerging from the central supermassive black hole in M87; it is more than 100,000 light years long!. |
 The quasar #c273, at a distance of 3 billion light yrs. This was the first quasar to be discovered. All we see here is the central core and the 120,000 light-yr long jet - the rest of the galaxy is too faint to be seen. |
|
Now supermassive black holes are not the only black holes around - indeed, our own galaxy, along with all other galaxies, is certainly full of many smaller ones, of masses from roughly 2-20 solar masses, these being the leftover cores that remain after a supergiant star explodes as a supernova at the end of its life. Although this is something that happens to only a small fraction of really massive stars in any galaxy, it has happened to roughly 100 million such stars already in the Milky Way's lifetime - our galaxy contains some 200 billion stars. Thus we may expect such objects - supernovae remnants - to be scattered around our galaxy, with a typical distance of roughly 100 light years between them. Of course not all of these supernovae will leave behind a black hole - the majority will instead leave a rapidly expanding cloud (the outer parts of the star) plus a neutron star, which is the remains of the central core of the star, now collapsed to incredibly high nuclear densities (densities so high that an object the size of a sugar cube, made from nuclear matter, would have a mass roughly that of Grouse Mountain). However if the neutron star is too massive, it must collapse to a black hole. Most of these black holes will be quite undetectable - after all, nothing, not even light, can escape from them! To see any sign of them we need matter to be falling into them - as it falls in, it will release enormous quantities of energy, mostly along the axis of rotation of the black hole, which we see as the jets. |
||
 ABOVE LEFT: the first stellar-mass black hole to be discovered, Cygnus X1 (the X-ray emission gave it away). ABOVE RIGHT: An artist's depiction of Cygnus X1 - a supergiant star orbits a black hole (itself formed when another supergiant exploded). The black hole is busy sucking matter from the outer parts of the supergiant into an 'accretion disc' around it - as matter falls into the black hole from this disc, enormous energy is emitted along the axes - these are the 'jets'. |
 The famous "Crab nebula" M1, visible in a small telescope. This is the expanding remnant from a supernova which was seen by Chinese observers in 1058 AD. It is 6,000 light years away, but it far outshone the stars and planets in our sky at that time. |
|
| Now the actual processes occurring in the vicinity of a black hole are very messy, but the basic pattern is the same, whether we are dealing with a supernova remnant or a supermassive black hole in a galactic core. Matter of one kind or another spirals into the spinning black hole, initially into an 'accretion disc' around it - friction in the accretion disc and massive acceleration of the matter as it approaches the event horizon then lead to huge energy output. Almost all of this energy is focussed along 'relativistic jets' directed along the axis of rotation (this is mainly because of the structure of the Kerr spacetime around the black hole), and much of this energy is initially in the form of X-rays. Since X-rays do not penetrate the earth's atmosphere, these systems were undetected until military satellites saw them. | ||
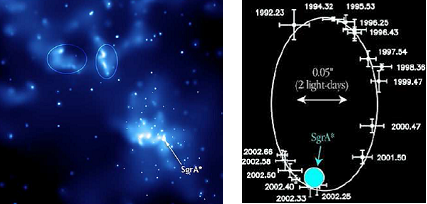 ABOVE LEFT: The region of the centre of Milky Way where resides - this is a strong source of radio waves. ABOVE RIGHT: Orbit of one of the stars near Sgr A - it is moving so fast around Sgr A (12,000 km/sec at its fastest) that it takes only 30 yrs to perform a complete circuit. |
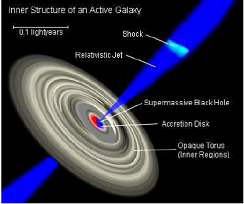 Structure of the region around a supermassive black hole. The accretion disc extends over nearly a light yr, and any radiation trying to escape in the ring plane is blocked by the disc. |
|
The radiation intensity in the jets from supermassive black holes is enormous - they can outshine entire galaxies by a factor of at least a thousand! And yet the radiation is coming from a very small region, maybe only a few light hours or a light day across (1 light-hour is a little over the distance from the sun to Jupiter). Hence they can fluctuate in intensity over only a few hrs. That quasar light was seen to do this in the 1960s was a huge mystery at that time - it seemed impossible to explain such a colossal energy source that was so small. Notice of course that none of these black holes, in this picture, can emit anything if there is no matter around them to spiral in. This is why our own Milky Way supermassive black hole is so benign - not only is it rather lightweight, but it has already absorbed most of its immediate vicinity. The next chapter in this saga came when theoretical physicists asked what would happen when one tried to mix quantum mechanics up with General Relativity. The first breakthrough came in the early 1970's, when Stephan Hawking came to the remarkable conclusion that even a black hole in empty space could emit radiation, which would look like thermal 'black-body' radiation, from an object at a finite temperature (the 'Hawking temperature'). The 'stretching' of spacetime around the black hole allowed it to destabilize even the vacuum, through a purely quantum process which resembles quantum tunneling. This Hawking radiation would cause it to lose mass - eventually it would evaporate away. In a related development Bill Unruh showed that an object accelerating through a vacuum would feel thermal 'Unruh radiation' at the 'Unruh temperature' - even empty spacetime would appear to be stretched and hot if you accelerated through it. Hawking and others (Bekenstein, and later Unruh, Wald, etc) also showed that black holes contain a huge amount of entropy (entropy is a measure of the total number of different possible states the object can exist in). In fact we now know that the fraction of the entropy in the universe that is NOT contained in black holes is only about 1 part in 1016 !! From this point of view, black holes really do control the universe - they have come very far in our eyes from being just a mathematical curiosity, or a 'theoretical abomination'. And this takes us up to present research - because we cannot understand any more about black holes until we have a proper theory of quantum gravity - the biggest problem currently facing physics. For more on this see biggest problem, and quantum gravity. FURTHER READING Any real explanation of Black Holes is pretty messy - the curvature mixes up space and time, and things get very complex. If you are interested in learning more, without needing to know all this complexity, go to GR-Spacetime, and/or to articles on Wikipedia. |
||